Vacío en Lacan y vacío lógico: de Aristóteles y Frege al sujeto en Psicoanálisis
El vacío en Lacan no es una metáfora ni una intuición clínica, sino un problema lógico que atraviesa distintas tradiciones del pensamiento. A lo largo de este texto, el recorrido se organiza paso a paso para mostrar cómo la noción de vacío lógico se articula desde Aristóteles y Frege hasta convertirse en un concepto central para pensar el sujeto en el psicoanálisis.
A través de la lógica clásica, la lógica moderna y la teoría lacaniana, se pone en evidencia cómo el vacío deja de ser un límite del pensamiento para funcionar como una condición estructural: primero en la formalización del número y, luego, en la concepción del sujeto, la falta y el deseo.
Qué significa “vacío” en Lacan
En Lacan, vacío no nombra un hueco psicológico ni una carencia empírica, sino una función estructural. La idea central es que el sujeto no coincide consigo mismo como una sustancia plena: aparece como un efecto del lenguaje, y ese efecto se sostiene en una falta constitutiva.
Por eso, hablar del vacío en Lacan implica ubicar un punto de imposibilidad: algo del sujeto no puede quedar totalmente representado en el significante. Esta imposibilidad no es un defecto accidental, sino una condición de la estructura simbólica. En términos lacanianos, ese vacío se articula con la falta, el deseo y la relación con el Otro.
En este sentido, el “vacío” funciona como un operador: marca el lugar donde la formalización toca un límite y, al mismo tiempo, hace posible una serie de efectos (deseo, demanda, sustituciones significantes). A partir de aquí se vuelve decisivo el pasaje por la lógica: la pregunta por “lo propio de ninguno”, la clase vacía y el cero permiten precisar que el vacío no es una ausencia cualquiera, sino un punto que estructura.
Universal, particular y singular en Aristóteles
Para situar el problema del vacío lógico, es necesario partir de la distinción entre universal, particular y singular en Aristóteles. Estos conceptos organizan su lógica y su metafísica, y delimitan qué puede y qué no puede pensarse dentro de su sistema.
El universal es aquello que puede predicarse de muchos. Por ejemplo, “animal” es un universal porque se dice de múltiples seres. El particular designa una clase dentro del universal, como “hombre” dentro de “animal”. El singular, en cambio, remite a lo individual irrepetible: “Sócrates”, este cuerpo, este ente concreto.
Esta jerarquía establece un orden claro: lo universal se dice de muchos, lo particular agrupa, y lo singular designa lo que es propio de uno solo. Sin embargo, esta misma lógica deja planteada una pregunta límite: si lo singular es lo propio de uno, ¿es posible pensar algo que sea propio de ninguno?
Ese punto marca un borde del sistema aristotélico. Allí donde la lógica clásica solo reconoce lo que puede predicarse de algo, comienza a insinuarse un problema que Aristóteles no formaliza como tal, pero que será decisivo para la lógica moderna y, más adelante, para Lacan.

Universal, particular y singular: la lógica clásica
El universal es aquello que puede predicarse de muchos; designa una categoría general que reúne múltiples casos. El particular corresponde a una clase más específica dentro de ese universal. El singular, en cambio, remite a lo individual irrepetible: aquello que no se predica de nada más y existe como realidad concreta.
Esta organización establece un orden preciso: lo universal se dice de muchos, lo particular agrupa a los singulares, y lo singular es siempre lo propio de uno solo. Sin embargo, esta misma lógica deja planteado un límite decisivo: si lo singular es lo propio de uno, ¿cómo pensar algo que sea propio de ninguno?
Ese punto marca el borde del sistema aristotélico. Allí donde la lógica clásica solo reconoce lo que puede predicarse de algo, comienza a insinuarse un problema que no puede resolverse dentro de su marco, pero que será central para la lógica moderna y, más adelante, para la concepción lacaniana del sujeto.
El límite del sistema aristotélico
Sin embargo, esta misma lógica deja planteado un límite decisivo: si lo singular es lo propio de uno, ¿cómo pensar algo que sea propio de ninguno?
Ese punto marca el borde del sistema aristotélico. Allí donde la lógica clásica solo reconoce lo que puede predicarse de algo, comienza a insinuarse un problema que no puede resolverse dentro de su marco, pero que será central para la lógica moderna y, más adelante, para la concepción lacaniana del sujeto.
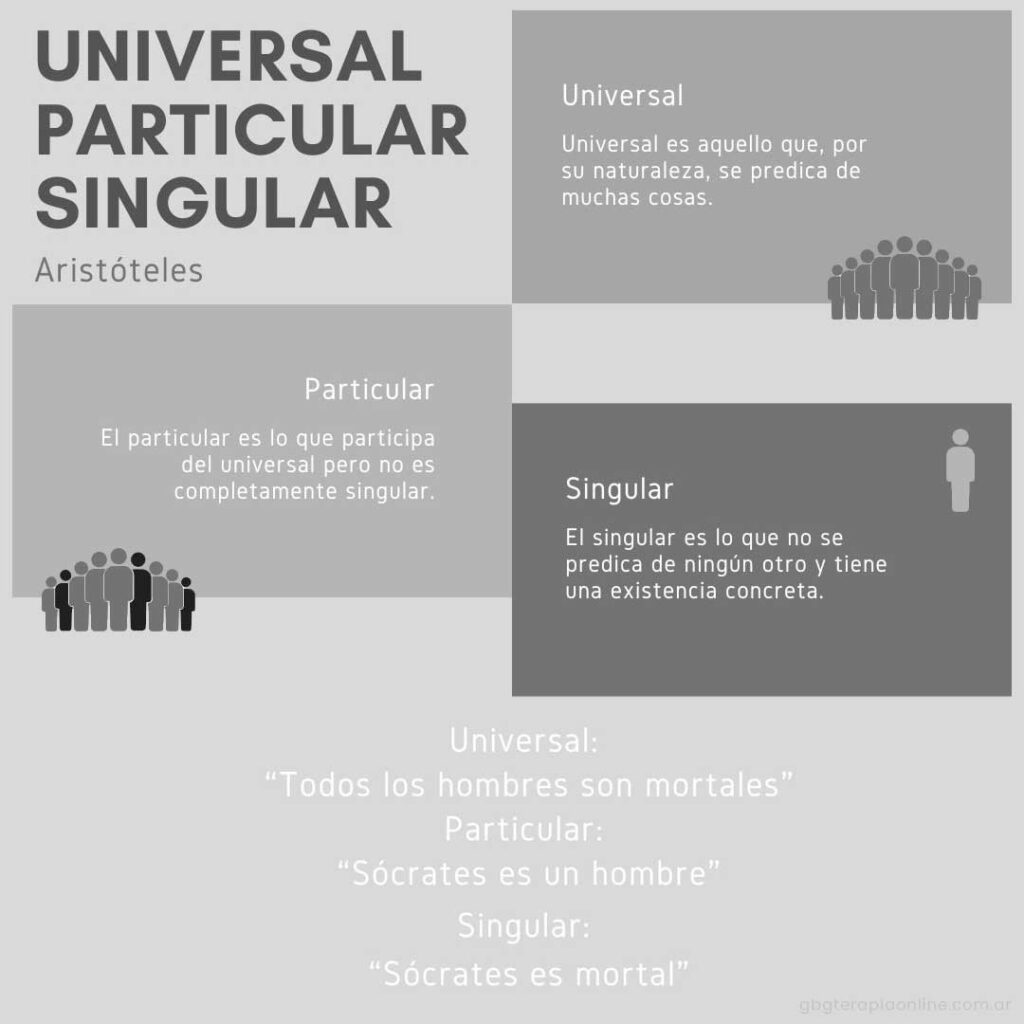
Relación entre Universal, Particular y Singular
Desde el punto de vista epistemológico, Aristóteles sostiene que el conocimiento humano comienza en la percepción de lo singular y alcanza lo universal mediante la abstracción. Por ejemplo, al observar muchos árboles concretos, el intelecto abstrae la idea de “árbol” como concepto universal, reconociendo aquello que se repite más allá de cada caso particular.
En el plano metafísico, los singulares constituyen las sustancias primeras, es decir, las realidades concretas que existen efectivamente, mientras que los universales poseen una existencia secundaria como formas o conceptos inteligibles. Esta distinción refuerza la primacía de lo singular en el orden del ser y del conocimiento.
Ahora bien, definir lo singular como aquello que es propio de uno solo abre una pregunta decisiva: ¿es posible concebir algo que sea propio de ninguno? En el sistema aristotélico, todo lo que existe mantiene alguna relación con el ser, ya sea como sustancia, accidente o privación. Plantear lo propio de ninguno introduce así una tensión en el marco clásico y anticipa el problema del vacío lógico, que reaparecerá en la noción de clase vacía en Frege y, más adelante, en la concepción lacaniana de la falta estructural.
Cómo se enfrentaría Aristóteles a lo propio de ninguno
En el marco de la lógica aristotélica, los conceptos de universal, particular y singular organizan de manera coherente el pensamiento y la experiencia.
Lo universal se predica de muchos; lo particular participa de ese universal sin ser único; y lo singular designa aquello que es propio de uno solo y existe como realidad concreta.
Esta articulación no solo ordena el pensamiento lógico, sino que también explica cómo se estructura el conocimiento humano: comienza en lo individual, pasa por lo específico y alcanza lo abstracto. Sin embargo, esta misma organización deja planteada una pregunta límite, que no puede resolverse dentro del propio sistema.
Lo propio de ninguno en Aristóteles
La idea de algo que sea “propio de ninguno” no tiene cabida en el pensamiento de Aristóteles, ya que su sistema filosófico se funda en una lógica del ser y del conocimiento.
Todo lo que existe debe poseer algún tipo de determinación: como singular, particular o universal.
Plantear algo que no sea propio de nadie ni de nada introduce una dificultad radical. Aunque la pregunta puede formularse, no puede integrarse como concepto dentro del marco aristotélico sin poner en cuestión sus principios fundamentales.
La Lógica de Aristóteles y lo “propio de ninguno”
La exclusión de lo “propio de ninguno” se apoya en el principio de no contradicción, eje central de la lógica aristotélica: algo no puede ser y no ser al mismo tiempo y en el mismo sentido.
Por ello, si algo es, necesariamente debe ser algo determinado, es decir, poseer una esencia o pertenecer a alguna categoría del ser.
En este marco, lo universal es siempre “propio de muchos” y lo singular es “propio de uno”. Algo que fuera “propio de ninguno” implicaría una carencia total de determinación y, por lo tanto, una forma de no-ser, que Aristóteles excluye como imposible.
Lo “propio de ninguno” y el No-Ser
En la Metafísica, Aristóteles analiza el concepto de no-ser, especialmente en su discusión con Parménides. El no-ser no puede existir en sentido absoluto; solo puede pensarse de manera relativa, como negación o privación de una propiedad determinada.
Decir que algo “no es hombre” o “no es rojo” no introduce una entidad nueva, sino que señala la ausencia de una cualidad específica. En cambio, algo que fuera absolutamente “propio de ninguno” equivaldría a no existir en absoluto.
Desde el punto de vista metafísico, aquello que no posee ninguna determinación —ni siquiera la de ser singular o universal— no puede ser considerado un ente.
El Concepto de Materia Prima
Una noción que podría parecer cercana a la idea de “propio de ninguno” es la de materia prima (hýlē). Para Aristóteles, la materia prima es pura potencia y carece de forma propia.
Sin embargo, no existe nunca de manera independiente.
La materia prima no es un ser en sí mismo, sino un principio metafísico que solo adquiere entidad al unirse con una forma. Sin forma, sería indeterminada; pero Aristóteles insiste en que no puede haber materia sin forma en el mundo real. Por eso, tampoco aquí aparece un verdadero vacío.
Lo Vacío o el Espacio como “Propio de Ninguno”
En algunos pasajes de la Física, Aristóteles examina la noción de vacío entendida como espacio absolutamente vacío. Su conclusión es clara: tal vacío no existe, ya que el espacio siempre está ocupado por alguna sustancia.
Un vacío absoluto equivaldría al no-ser y, por lo tanto, carecería de propiedades. De este modo, incluso en el plano físico, Aristóteles rechaza la posibilidad de algo que sea completamente “propio de ninguno”.
Aristóteles y la existencia conceptos de dimensión vacía
Aunque Aristóteles excluye el vacío como realidad independiente, reconoce en sus tratados lógicos la existencia de ciertos conceptos que, desde una perspectiva moderna, podrían describirse como pertenecientes a una dimensión vacía.
Estos conceptos no ocupan un lugar central en su sistema, pero aparecen como efectos secundarios del lenguaje y del razonamiento lógico.
1. La Privación como Concepto Lógico
La privación (stérēsis) designa la ausencia de una propiedad esperable. No introduce un ser positivo, pero puede funcionar como predicado lógico, señalando una falta dentro de la naturaleza de un sujeto.
2. La Noción de Negaciones Absolutas
En los Analíticos Primeros, Aristóteles examina proposiciones negativas que parecen estar asociadas con conceptos vacíos o sin contenido real. Estas proposiciones pueden referirse a lo que no existe o a conceptos que no tienen correlato en la realidad.
- Ejemplo lógico: «El unicornio no es un animal real.»
- Aunque el término «unicornio» tiene una estructura conceptual (es un animal con un cuerno etc), carece de existencia concreta en la realidad.
- Aristóteles permite el uso de términos vacíos en los juicios negativos, pero los considera secundarios y subordinados al conocimiento de lo que existe.
3. La Contradicción y los Conceptos Vacíos
En su lógica, Aristóteles analiza el principio de no contradicción (Metafísica, Libro IV) y establece que no puede haber algo que simultáneamente sea y no sea. Sin embargo, esto lo lleva a reflexionar sobre proposiciones contradictorias que parecen referirse a una «dimensión vacía».
- Ejemplo de contradicción lógica: «Un círculo cuadrado.»
- Esta proposición no se refiere a nada real, ya que el concepto de «círculo cuadrado» es inherentemente contradictorio.
- Aristóteles trata estos conceptos como meras combinaciones de términos lingüísticos que no tienen correspondencia en la realidad.
Para él, estas ideas son lógicamente posibles como construcciones mentales, pero metafísicamente son inexistentes.
4. Los Conceptos Matemáticos y el Vacío
En sus obras sobre filosofía natural, como la Física, Aristóteles se ocupa de los conceptos matemáticos abstractos, algunos de los cuales podrían ser considerados «vacíos» en términos de su aplicabilidad al mundo físico.
- Ejemplo: El concepto de «punto» en geometría.
- Un punto no tiene dimensión, masa ni extensión; es una entidad abstracta que no existe físicamente, pero es útil en el razonamiento matemático.
- Aristóteles acepta que estos conceptos abstractos tienen validez en sus propios sistemas lógicos, pero no los considera parte de la realidad material.
5. Los Términos Universales Vacíos
En los Analíticos Segundos, Aristóteles menciona que existen términos universales que no se aplican a ningún individuo real, pero que tienen sentido lógico.
- Ejemplo lógico: «El fénix es un ave.»
- Aunque «fénix» no corresponde a ninguna ave existente, el término puede ser usado en proposiciones que tienen una estructura lógica válida.
Aristóteles distingue entre el uso de términos vacíos en el lenguaje y la existencia real de aquello a lo que estos términos podrían referirse.
6. La Dimensión Vacía en el Sentido Potencial
Otro aspecto interesante es el concepto de potencia en Aristóteles. Algo que está en potencia, pero no en acto, podría parecer «vacío» desde un punto de vista actual.
- Ejemplo metafísico: Una semilla que tiene el potencial de convertirse en árbol, pero que aún no lo es.
- En este estado, la semilla contiene una capacidad que no está realizada. Podría interpretarse como algo «vacío» en acto, pero lleno de posibilidad en potencia.
Aristóteles reconoce, entonces, ciertos conceptos que pueden pensarse como vinculados a una dimensión vacía, pero siempre de manera secundaria.
La privación, las negaciones, las contradicciones, los conceptos matemáticos abstractos y la potencia no constituyen un vacío estructural, sino efectos marginales dentro de un sistema que privilegia el acto, la sustancia y la determinación. Por esta razón, el vacío no puede ocupar un lugar fundante en la filosofía aristotélica. Ese límite interno será precisamente el punto a partir del cual la lógica moderna y, más adelante, el psicoanálisis lacaniano, elaborarán una concepción distinta del vacío.
Aunque Aristóteles no explora explícitamente la idea de vacío lógico, su tratamiento del «no-ser» como privación abre una puerta. Esta ausencia estructural será fundamental para Frege y, más adelante, para Lacan.
El vacío y su incorporación en la lógica moderna
La cuestión del vacío y su incorporación en la lógica moderna, a partir de Charles Sanders Peirce y Gottlob Frege, representa un cambio radical respecto de la lógica aristotélica.
Mientras Aristóteles se centró en conceptos aplicables al mundo real y dejó fuera los términos sin extensión, la lógica moderna incorporó explícitamente el vacío, el conjunto vacío y el cero como conceptos fundamentales para la formalización matemática y lógica.
1. Charles Sanders Peirce y la Extensión Vacía en la Silogística
Charles Sanders Peirce, uno de los fundadores de la lógica moderna, revisó la silogística aristotélica y amplió su alcance al incorporar términos sin extensión y conjuntos vacíos dentro del razonamiento lógico.
Silogística Aristotélica y Extensión Vacía
Aristóteles excluía los términos sin extensión —aquellos que no refieren a nada existente— porque su lógica se apoyaba en conceptos con correlato real.
Peirce, en cambio, sostuvo que los términos vacíos no solo son legítimos, sino que modifican la estructura misma de los razonamientos lógicos.
Conjuntos Vacíos y Relaciones Silogísticas
En la lógica moderna, un conjunto vacío designa una clase que no contiene elementos. Por ejemplo, “unicornio” es un término vacío, ya que no existen unicornios en la realidad.
Peirce mostró que incluir términos vacíos altera las relaciones silogísticas tradicionales. En un razonamiento como:
– “Todos los unicornios son animales mitológicos”
– “Algunos unicornios son blancos”
la validez lógica ya no depende de la existencia real del término, sino de su función dentro del sistema formal.
Impacto de Peirce
Con estas reformulaciones, Peirce introdujo una lógica cuantificacional capaz de evaluar proposiciones incluso cuando sus términos no refieren a entidades reales. Su trabajo abrió el camino hacia sistemas formales más generales y sentó bases decisivas para la lógica matemática contemporánea.
2. Gottlob Frege y el Fundamento Lógico de la Aritmética
Gottlob Frege buscó proporcionar una fundamentación lógica de la aritmética, mostrando que los números podían definirse a partir de relaciones lógicas y conjuntos, sin recurrir a intuiciones matemáticas previas.
La Serie Numérica y el Concepto de Cero
Frege, en Los Fundamentos de la Aritmética (Die Grundlagen der Arithmetik), buscó mostrar cómo los números podían definirse mediante relaciones lógicas y conjuntos, especialmente considerando el conjunto vacío como punto de partida.
El concepto del número 0:
- Frege definió el número 0 como la «clase vacía», es decir, el conjunto que no contiene ningún elemento.
- Esto conecta la noción de «extensión vacía» con la aritmética: el cero no es simplemente un número, sino una construcción lógica basada en la ausencia de elementos.
El número 1 y los siguientes:
- El número 1 se define como la clase que contiene al conjunto vacío.
- El número 2 se define como la clase que contiene tanto al conjunto vacío como al conjunto que contiene al conjunto vacío.
- Así, Frege creó una serie numérica basada en la lógica pura y la construcción de conjuntos, sin recurrir a intuiciones matemáticas tradicionales.
Proposiciones y Funciones
Frege utilizó su noción de funciones y valores-verdad para explicar cómo los números operan en estructuras lógicas. Por ejemplo:
- Una función como f(x)=x+1 no depende de elementos concretos, sino de relaciones lógicas entre conjuntos.
- Esto permitió una generalización de la aritmética y sentó las bases para la lógica matemática moderna.
El Impacto de Frege
- Redujo los números a conceptos puramente lógicos, lo que permitió vincular la matemática con sistemas lógicos formales.
- Su trabajo influyó profundamente en Bertrand Russell y Ludwig Wittgenstein, y más tarde en el desarrollo de la teoría de conjuntos.
Diferencias Peirce y Frege con Aristóteles
- Aristóteles:
- La lógica es un reflejo del mundo real y se centra en términos con extensión real.
- No trabaja con la noción de vacío ni con abstracciones matemáticas.
- Peirce y Frege:
- La lógica incluye términos sin extensión y conjuntos vacíos como componentes fundamentales.
- El vacío no es un problema filosófico, sino una herramienta lógica y matemática.
Peirce y Frege
Ambos abrieron el camino hacia una lógica formal mucho más abstracta que la aristotélica:
- Peirce lo hizo extendiendo las relaciones entre términos vacíos y su impacto en la lógica proposicional y cuantificacional.
- Frege utilizó estas nociones para redefinir los fundamentos de la matemática.
La incorporación de conceptos como el conjunto vacío y la serie numérica lógica marca una ruptura con la lógica de Aristóteles:
- Peirce transformó la silogística tradicional al incluir términos vacíos, expandiendo su aplicabilidad a sistemas formales abstractos.
- Frege utilizó estos conceptos para proporcionar un fundamento lógico a la aritmética, mostrando que los números pueden construirse desde principios puramente lógicos.
Ambos autores sentaron las bases de la lógica y la matemática modernas, mostrando que incluso conceptos vacíos o abstractos pueden tener un lugar central en el razonamiento lógico.
Frege y el fundamento lógico del número
Frege aborda el concepto de vacío y su relación con el número cero de manera innovadora en su obra Die Grundlagen der Arithmetik (Los Fundamentos de la Aritmética), en la cual busca establecer una fundamentación lógica de los números y la serie numérica. Aquí se explican los aspectos clave del enfoque de Frege sobre el cero, su conexión con el vacío, y cómo este concepto permite construir la serie numérica.
1. El Cero como Clase Vacía
Frege define el número cero en términos puramente lógicos, a partir del concepto de clase vacía. Este es el punto de partida de su sistema:
¿Qué es la clase vacía?
- La clase vacía es el conjunto que no contiene ningún elemento. Es la representación lógica de la «nada» o del «vacío».
- En términos formales: ∅={}.
El cero como la clase vacía:
- Para Frege, el número cero no es simplemente una cantidad ni una representación abstracta, sino un concepto lógico que denota la ausencia de objetos.
- El cero es el cardinal (número de elementos) de la clase vacía: Card(∅)=0.
2. La Generación de la Serie Numérica
A partir del concepto de vacío y del número cero, Frege construye la serie numérica utilizando relaciones lógicas y conjuntos.
El Número Uno
Frege define el número uno como la clase que contiene al cero (es decir, a la clase vacía):
- Formalmente:
- 1={∅}
- Esto significa que el número uno es el conjunto que tiene como único elemento a la clase vacía.
El Número Dos
El número dos es definido como la clase que contiene al número uno y a la clase vacía:
- Formalmente:
- 2={∅,{∅}}
- En este caso, el número dos es el conjunto que contiene dos elementos: la clase vacía (∅) y la clase que contiene la clase vacía ({∅}).
El Número Tres y los Siguientes
El número tres se define de manera similar, como el conjunto que contiene al número dos, al número uno y al número cero:
- Formalmente:
- 3={∅,{∅},{∅,{∅}}}
3. La Función Sucesor
Frege introduce una función sucesor (S) para formalizar la generación de la serie numérica. Esta función toma un número n y produce el siguiente número en la serie:
- S(n)=n∪{n}
- Esto significa que el sucesor de un número n es el conjunto que incluye todos los elementos de n, además de n mismo como un nuevo elemento.
Ejemplo con el número 2:
- S(2)=2∪{2}
- S(2)={∅,{∅}}∪{{∅,{∅}}}
- S(2)={∅,{∅},{∅,{∅}}}
- Esto corresponde al número 3.
4. Cero como Fundamento Lógico
Frege establece el número cero como el fundamento lógico de la aritmética porque:
Representa el punto de partida de la serie numérica:
- El cero, como la clase vacía, es el primer concepto cardinal y no depende de otros números.
Define los números como conjuntos:
- Cada número se construye inductivamente a partir del cero y la función sucesor. Esto permite que toda la serie numérica esté fundamentada en relaciones puramente lógicas.
Conecta la lógica y la matemática:
- Al definir los números como clases y la serie numérica como una estructura generada lógicamente, Frege elimina la necesidad de intuiciones matemáticas independientes de la lógica.
5. El Cero como “Uno”
Frege, en cierto sentido, otorga al cero un estatus similar al de un «uno» lógico, porque es el primer paso necesario para construir la serie numérica:
- El cero funciona como el primer elemento o base en la construcción de los números.
- A partir del cero, los números se generan como «clases de clases», en una estructura acumulativa.
6. Importancia de este Enfoque
Frege no solo redefine el cero como un concepto lógico, sino que transforma la comprensión de los números al vincularlos con la teoría de conjuntos y la lógica formal:
La Aritmética se vuelve un subconjunto de la Lógica:
- Frege muestra que los números son constructos lógicos y no conceptos independientes.
Introducción del Vacío como Concepto Central:
- Al definir el cero como clase vacía, Frege pone al vacío en el centro de la lógica matemática, en contraste con Aristóteles, quien lo excluyó.
Base para la Lógica Matemática Moderna:
- Este enfoque influyó en el desarrollo de la teoría de conjuntos por Cantor y en los sistemas formales de Russell y Whitehead en Principia Mathematica.
Para Frege, el cero no es solo un número, sino el fundamento lógico que permite construir toda la serie numérica. Su definición como clase vacía conecta el vacío con las bases de la aritmética y demuestra que los números no necesitan una intuición matemática previa, sino que emergen de principios lógicos y relaciones entre conjuntos. Este enfoque no solo amplió la lógica, sino que transformó la comprensión matemática de los números y sentó las bases para la matemática moderna.
Vacío lógico en Frege y Lacan
Tanto Frege como Lacan reconocen que el vacío tiene un papel estructurante. Sin embargo, mientras Frege lo utiliza para construir los números, Lacan lo convierte en el núcleo del sujeto.
La extensión del vacío en la lógica
Frege demuestra que el vacío no es una carencia, sino un fundamento. Es lo que permite generar la serie numérica y establecer relaciones lógicas precisas. Esto conecta directamente con la falta estructural en Lacan.
Jacques Lacan, en su desarrollo de la teoría psicoanalítica, toma ciertos conceptos de la lógica y las matemáticas, como los fundamentos lógicos de los números en Frege y las nociones de vacío y estructura, para construir su concepción del sujeto. Lacan transforma estas ideas en un marco teórico psicoanalítico que conecta lógica, lenguaje y subjetividad. A continuación, se detalla cómo Lacan relaciona estas nociones con su idea del sujeto.
1. La Influencia de la Lógica y el Vacío en Lacan
Lacan adopta la noción de vacío lógico para explorar el estatuto del sujeto como algo que no está plenamente presente en el ser, sino que surge como una falta o vacío dentro del orden simbólico. Algunos puntos clave de esta influencia:
El vacío lógico y el sujeto barrado $:
- Al igual que el «0» en Frege representa la clase vacía, Lacan utiliza la idea del vacío para describir al sujeto como una falta estructural. El sujeto no es un ente positivo o plenamente identificable, sino un efecto de la estructura simbólica (el lenguaje).
- El sujeto está marcado por una imposibilidad de ser completamente representado en el lenguaje.
La lógica del significante:
- Lacan sostiene que el sujeto es un efecto del significante, y el significante funciona en una cadena que nunca nombra completamente al sujeto. Aquí podemos ubicar la idea de Frege de que el número y las operaciones no existen en sí mismos, sino como relaciones dentro de un sistema lógico.
2. La Serie Numérica y el Orden Simbólico
Frege define los números a partir de relaciones lógicas entre clases y conjuntos, comenzando con el cero como clase vacía. Lacan toma esta idea estructural para teorizar al sujeto dentro del orden simbólico – el lenguaje y las leyes que estructuran la cultura.
El sujeto como parte de una serie:
- Lacan compara al sujeto con un elemento de una serie lógica: siempre definido en relación con otros significantes, pero nunca independiente ni autosuficiente.
- Como en la lógica de Frege, donde «1» no puede definirse sin «0», el sujeto lacaniano no puede existir sin referencia al Otro (el lenguaje y el contexto social).
El «cero» como falta estructural:
- Así como Frege utiliza el «cero» como fundamento de la serie numérica, Lacan utiliza la falta como el fundamento del sujeto. El sujeto no es pleno ni autónomo porque siempre está determinado por algo que falta: su relación con el deseo del Otro.
3. El Sujeto Dividido y la Función Sucesor
En la lógica de Frege, el sucesor (S(n)) define cómo se genera la serie numérica, basándose en la acumulación de lo que ya está dado. Lacan utiliza una idea similar para describir el desplazamiento del sujeto dentro de la cadena significante:
El sujeto como sucesor incompleto:
- Cada significante (como el número en Frege) apunta al siguiente, pero nunca agota el significado del sujeto. Esto implica que el sujeto es siempre incompleto, como un «sucesor lógico» que nunca alcanza un punto de plenitud.
El «plus de goce» como acumulación:
- En términos del deseo y el goce, el sujeto siempre busca «algo más» (un excedente, objeto a) que nunca puede ser plenamente alcanzado, similar a cómo en la lógica de Frege, la serie numérica siempre puede extenderse pero nunca culmina en un todo absoluto.
4. La Relación entre Cero y Uno: La División del Sujeto
Frege muestra que «1» depende de «0», y Lacan adopta esta relación para describir la división del sujeto entre ser y no-ser:
El «cero» como representación del no-ser:
- Lacan conecta el vacío lógico de Frege con la falta en el sujeto. Esta falta es estructural, no algo que se pueda «llenar», porque es lo que define al sujeto como tal.
El «uno» como intento de simbolización:
- El sujeto intenta representarse a sí mismo en el lenguaje, pero esta representación es siempre parcial. Así como «1» depende del «0» en Frege, el sujeto depende de su falta estructural para definirse.
5. El Cálculo Formal y el Sujeto del Inconsciente
Lacan ve el inconsciente como estructurado como un lenguaje, lo que lo lleva a incorporar herramientas lógicas y matemáticas para explicar su funcionamiento:
El inconsciente estructurado como un lenguaje:
- Así como Frege formaliza la lógica para demostrar que los números son relaciones, Lacan describe al sujeto como una relación entre significantes. El sujeto no existe fuera del lenguaje, sino que es un «efecto» de este.
El significante vacío:
- Lacan introduce la idea del significante vacío [significante de la falta en el Otro], que no se refiere a ningún contenido específico, pero organiza la cadena significante. Este concepto tiene ecos de la clase vacía en Frege, donde el «cero» estructura el sistema numérico sin representar nada concreto.
6. El Fundamento Lógico del Sujeto Lacaniano
Al igual que Frege busca el fundamento lógico de los números en conceptos básicos como la clase vacía y la función sucesor, Lacan busca el fundamento del sujeto en la relación entre la falta, el lenguaje y el deseo:
El sujeto como vacío fundante:
- El sujeto es un vacío estructural que permite el funcionamiento del lenguaje y la simbolización, similar al «0» en Frege.
El Otro como sistema lógico:
- El Otro es el lugar del lenguaje y las leyes simbólicas que estructuran al sujeto, análogo al sistema lógico de Frege donde cada número existe solo en relación con los demás.
Conclusión: El vacío como clave para el sujeto
La noción de vacío lógico, la dependencia estructural entre los elementos de un sistema y el papel del «0» como base para construir su teoría del sujeto. Para Lacan, el sujeto no es una entidad completa ni autónoma, sino una falta estructural que se inscribe en el orden simbólico. Esta falta se parece al «vacío» que Frege coloca en el centro de la serie numérica, ya que es el punto de partida para toda significación y relación lógica. El sujeto lacaniano, como el sistema lógico de Frege, es relacional, incompleto y definido por su vínculo con lo ausente.
Desde Aristóteles hasta Lacan, el vacío ha pasado de ser un problema lógico a ser el centro de la subjetividad. En Lacan, el sujeto barrado refleja cómo el vacío estructura el deseo y la relación con el Otro. Esta falta, lejos de ser una debilidad, es lo que define al sujeto humano.

